Сверхпроводимость 1,5-го рода: ни два, ни полтора


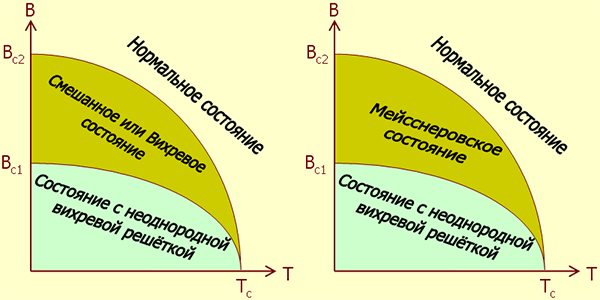
Рис. 5. Вероятные фазовые диаграммы сверхпроводников 1,5-го рода. Различия в поведении определяются параметрами двухщелевого сверхпроводника. Рисунок Юрия Ерина
Рис. 5. Вероятные фазовые диаграммы сверхпроводников 1,5-го рода. Различия в поведении определяются параметрами двухщелевого сверхпроводника. Рисунок Юрия Ерина

Таким образом, суммируя описанные выше факты, можно построить вероятные (на качественном уровне) фазовые диаграммы двухщелевых сверхпроводников (рис. 5), у которых параметры Гинзбурга–Ландау для каждой из двух разновидностей куперовских пар соответственно меньше и больше 1/v2. Подчеркнем еще раз, что при постепенном увеличении от нуля индукции магнитного поля фазовая диаграмма сверхпроводника с двумя щелями «стартует» не с мейсснеровской фазы, как это имело место в сверхпроводнике 1-го или 2-го рода, а сразу с неоднородного вихревого состояния.

Аргументы против существования сверхпроводимости 1,5-го рода

Как уже было сказано, количественный критерий деления сверхпроводников на 1-й и 2-й род проистекает из знака поверхностной энергии границы раздела «сверхпроводник — нормальный металл». Очевидно, что здесь возможны только два случая (вариант с нулем исключается): либо поверхностная энергия положительная, либо отрицательная. Поэтому этот критерий не изменится даже для двухщелевого сверхпроводника. Именно такой довод приводится в статье Interface energy of two band superconductors, опубликованной в журнале Physical Review B. Авторы работы, коллектив ученых из США и ЮАР, фактически проделали те же расчеты, что и Абрикосов, но для сверхпроводника с двумя сортами куперовских пар. Они показали, что в случае, когда для первого сорта куперовских пар параметр Гинзбурга–Ландау меньше 1/v2, а для второго он больше 1/v2, поверхностная энергия принимает положительное значение, а потому имеет место сверхпроводимость 1-го рода.

Более того, те же ученые в другой своей статье доказывают, что различие между двумя разновидностями куперовских пар в температурном диапазоне в окрестности Tc, то есть там, где применяется теория Гинзбурга–Ландау, исчезает, и двухщелевой сверхпроводник превращается в сверхпроводник с одной щелью.

Чего ожидать дальше?

Все описанные здесь работы носят исключительно теоретический характер и основываются на численном анализе теории Гинзбурга–Ландау. Поставить точку в этом споре могут лишь очень аккуратные эксперименты по наблюдению вихревой решетки в двухщелевых сверхпроводниках. Благо сейчас стало известно, что не только диборид магния обладает двумя сортами куперовских пар, но и недавно открытые железосодержащие сверхпроводники (см. Открыт новый тип высокотемпературных сверхпроводников, «Элементы», 12.05.2008 и Найдено новое семейство сверхпроводников, содержащих железо, «Элементы», 31.10.2008), высококачественные монокристаллы которых синтезировать немного проще. Так что теперь с большой вероятностью следует ждать возврата дискуссии в экспериментальную плоскость.

Источники:
1) V. H. Dao, L. F. Chibotaru, T. Nishio, V. V. Moshchalkov. Giant vortices, vortex rings and reentrant behavior in type-1.5 superconductors // arXiv:1007.1849 (12 July 2010).
2) Shi-Zeng Lin, Xiao Huy. Vortex States and Phase Diagram of Multi-component Superconductors with Competing Repulsive and Attractive Vortex Interactions // arXiv:1007.1940 (12 July 2010).
3) Egor Babaev, Johan Carlstrom, Martin Speight. Type-1.5 Superconducting State from an Intrinsic Proximity Effect in Two-Band Superconductors // Phys. Rev. Lett. 105, 067003 (5 August 2010).
4) Jani Geyer, Rafael M. Fernandes, V. G. Kogan, Jorg Schmalian. Interface energy of two band superconductors // Phys. Rev. B 82, 104521 (27 September 2010); также доступна как arXiv:1007.2794.
5) V. G. Kogan, J. Schmalian. Two-band superconductors near Tc // arXiv:1008.0581 (3 August 2010).

Юрий Ерин

<< Назад