Поляризация света может закручиваться наподобие ленты Мёбиуса
|
Теоретический анализ так называемого трехмерного света показал, что направления поляризации в нём могут образовывать структуры с нетривиальной топологией, напоминающие ленту Мёбиуса.
Классическая оптика — это, казалось бы, очень «древний» раздел физики, однако и в нём время от времени обнаруживаются новые и подчас неожиданные явления. Взять например такую широко известную и изученную вдоль и поперек характеристику света, как поляризация. Можно ли в ней найти что-нибудь новое? Оказывается, да. В вышедшем на днях препринте рассказывается, что вектора поляризации в световой волне могут закручиваться наподобие ленты Мёбиуса — знаменитой поверхности, обладающей только одной стороной и только одной кромкой (см. рис. 1).
Для того чтобы объяснить суть открытия, начнем с пояснения, что такое поляризация света.
По своей физической природе свет — это электромагнитная волна, то есть поддерживающие друг друга колебания электрического и магнитного полей. По законам электродинамики вектор электрического поля должен всегда лежать в плоскости, перпендикулярной направлению движению световых лучей. Но колебаться электрическое поле в этой плоскости может по-разному, и слово «поляризация» как раз и обозначает тип колебания.
|
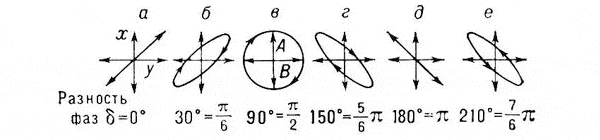
На рис. 2 показаны разные типы поляризации. Если колебания по оси x и y в этой плоскости происходят синхронно, то вектор электрического поля «вычерчивает» отрезок (рис. 1а и 1д), и такая поляризация называется линейной. Если колебание по одной из этих осей опережает другое ровно на четверть периода, то вектор электрического поля «вычерчивает» правильную окружность (рис. 1в), и такая поляризация называется круговой. А в общем случае получается нечто среднее — эллиптическая поляризация (см. рис. 1б, г, е). Эллиптическую поляризацию обычно изображают с помощью эллипса, причем чем больше его сплюснутость, тем ближе поляризация к линейной, а чем меньше сплюснутость — тем она ближе к круговой. Направление, вдоль которого эллипс вытянут, показывает, к какой именно линейной поляризации ближе всего данная эллиптическая поляризация. Анимацию колебаний электрического поля при всех трех типах поляризации можно посмотреть на странице Поляризация волн.
Всё вышеизложенное — физика XIX века, однако относятся эти рассуждения, строго говоря, только к плоским световым волнам (то есть к пучку строго параллельных лучей). Совершенно новые возможности открываются, когда лучи в световом пучке не параллельны, а направлены под большими углами друг к другу, как, например, в фокусе очень мощной линзы. Физики называют такой световой пучок трехмерным светом, и не зря. У разных лучей в этом пучке не не совпадают направления «вперед», а значит, не совпадают и плоскости поляризации. Получается, у всего светового пучка в целом уже нет какой-то определенной плоскости поляризации, и потому приходится следить за колебаниями электрического поля в трехмерном пространстве. Это приводит к таким экзотическим возможностям, как радиальная и продольная поляризации света. Кроме того, физики уже поняли, как в фокусе линзы ориентировать вектор поляризации вообще в произвольном направлении.
Оказывается, это еще не все возникающие возможности. В световом поле трехмерного света отдельные бегущие под углом друг к другу волны накладываются друг на друга в разных точках пространства по-разному. Из-за этого получается, что поляризация света плавно меняется от точки к точке — то есть возникает некоторое поле поляризаций.
|
Для того чтобы наглядно представить себе поле поляризаций и его необычные топологические свойства, вообразите некоторую плоскость, которая рассекает трехмерный световой пучок. Как уже говорилось, в каждой точке на этой плоскости отдельные световые лучи складываются по-своему, так что поляризация будет постепенно меняться от точки к точке. Если в какой-то точке она становится круговой, то в окрестности этой точки возникает интересная картина, схематично изображенная на рис. 3.
Здесь маленькие эллипсы показывают эллиптическую поляризацию света в данной точке, а стрелочки у каждого эллипса показывают направление большой полуоси. В центре имеется особая точка, в которой поляризация чисто круговая. Поскольку у окружности все направления равноправны, то в этой точке направления эллиптической поляризации просто не существует, оно не определено. Теперь взгляните на верхний эллипс, выделенный жирной красной линией, и проследите за ориентацией красных эллипсов при движении по кругу вокруг особой точки. Вы заметите, что за один оборот по кругу (то есть за поворот на 360°) направление эллипса поворачивается всего лишь на 180°. Полностью эллипс развернется только при двукратном обходе вокруг этой точки.
Иными словам, у каждого маленького эллипса нет однозначно определенной пары больших полуосей. Направление вправо при обходе вокруг особой точки плавно перетекает в направление влево в том же эллипсе. Поляризация света получается, в некотором смысле, неориентированной.
Отсюда до ленты Мёбиуса уже рукой подать. Представьте себе аналогичную ситуацию, но не на плоскости, а в пространстве. Если на плоскости была точка с круговой поляризацией, то в пространстве такие точки образуют линию. Вне этой линии поляризация эллиптическая, однако при обходе вокруг такой линии два направления эллипса переходят одно в другое ровно так же, как это происходит в ленте Мёбиуса.
|
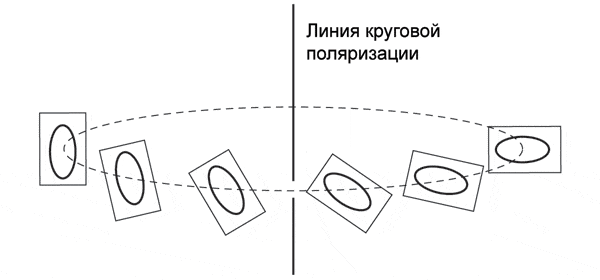
Один конкретный пример такой ситуации дан на рис. 4. Штриховой линией здесь показан путь, по которому мы обходим вокруг особой линии, а на некоторых точках этого пути схематично нарисованы эллипсы поляризации и плоскости, в которых эти эллипсы лежат. При таком обходе плоскость поляризации всегда смотрит на нас, но расположенный в ней эллипс постепенно поворачивается. Чтобы не загромождать картинку, показано лишь то, что происходит с поляризацией на половине пути — эллипс повернулся при этом на четверть оборота. Соответственно, при полном обходе вокруг особой линии эллипс повернется ровно на пол-оборота — точно так же, как разворачивается полоска в ленте Мёбиуса.
|
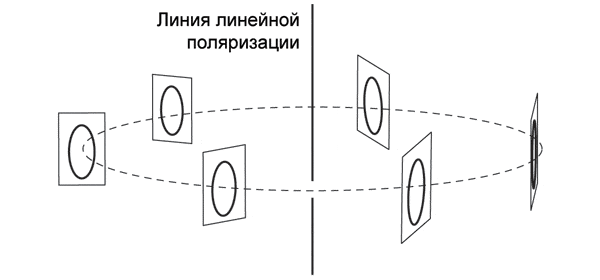
Это не единственная возможность. На рис. 5 показан другой случай, когда на пол-оборота поворачивается уже сама плоскость поляризации, а не эллипс в ней. Такая ситуация возможна при обходе вокруг линии не круговых, а линейных поляризаций. Кроме того, возможны случаи, когда поворачивается как плоскость поляризации, так и лежащий в ней эллипс, причем в разных направлениях и с разной «скоростью» (например, возможен аналог ленты Мёбиуса с тройным перекручиванием). В описываемом препринте, собственно, и были проклассифицированы все возможные типы таких топологически нетривиальных конфигураций.
Тут может возникнуть вопрос: является ли такая конфигурация экзотической, требующей специальных условий или же она возникает в трехмерном свете сама собой? Ответ на этот вопрос содержится в самом методе, с помощью которого автор препринта искал такие конфигурации. Он промоделировал наложение друг на друга 100 световых волн одинаковой длины волны, но с хаотично выбранными направлениями движения и с произвольно ориентированными линейными поляризациями. Оказалось, что в получившемся световом поле подобные конфигурации возникают с завидной постоянностью.
Осталось пояснить, какие перспективы сулит это открытие. Прежде всего, свет с экзотической поляризацией — это уникальный инструмент для воздействия на вещество, ведь электрическое поле разворачивает молекулы вдоль своего направления. Если физики научатся получать подобную «световую ленту Мёбиуса» в фокусе линзы, то благодаря ей можно будет топологически нетривиально поляризовать вещество, а возможно, даже порождать новые типы электромагнитных колебаний в материалах.
Во-вторых, с точки зрения математики сама по себе возможность возникновения таких структур вовсе не специфична для электромагнетизма. Нечто подобное следует искать и в других физических системах с векторными полями — в жидких кристаллах, в полях деформации упругих тел, в потоках жидкости. Кто знает, может быть нечто подобное существует даже на уровне элементарных частиц — в конце концов, в последние годы изучается возможность того, что глюонное поле способно завязываться в узлы и образовывать совершенно новый сорт частиц. Так это или нет — покажут дальнейшие теоретические исследования.
Источник: Isaac Freund. Optical Mobius Singularities // arXiv:0812.3263 (17 December 2008).
Игорь Иванов