Предсказан «эффект домино» в углеродных нанотрубках

Рис. 1. «Эффект домино» в углеродной нанотрубке (см. видео). (a) Начальная форма углеродной нанотрубки — цилиндрическая. (b) Один из концов трубки зажат двумя жестко двигающимися друг к другу узкими плоскостями графена (около 0,8 нм в ширину и 8,5 нм в длину). Под действием такого «пресса» рождается «эффект домино», приводящий к коллапсу нанотрубки с конечным расстоянием между противоположными стенками около 0,34 нм. (c) и (d) Распространение доминошной волны — конфигурации нанотрубки через 15 и 25 пикосекунд после сжатия ее конца. (e) Схематическая иллюстрация «эффекта домино» под действием силы тяжести. Рис. из обсуждаемой статьи в Physical Review Letters

Китайский физик Чжан Дяньчжонг теоретически предсказал существование «эффекта домино» в одностенной углеродной нанотрубке. Сжимая один из ее концов, можно наблюдать последовательное схлопывание участков такой структуры атомов углерода со скоростью, превышающей 1 км/с. Это явление происходит с выделением энергии, а значит, впервые позволяет говорить об углеродных нанотрубках как об источниках энергии. Этот эффект может быть также использован в качестве ускорителя молекул.

Оказывается, помимо известных вероятных применений углеродных нанотрубок — начиная с микроэлектроники и заканчивая экзотикой вроде проекта «космического лифта» — можно использовать такую форму объединения атомов углерода как источник энергии и даже как своеобразные ускорители молекул. Об этом идет речь в статье китайского физика из Шанхайского университета Чжана Дяньчжонга Dominoes in Carbon Nanotubes, опубликованной в журнале Physical Review Letters.

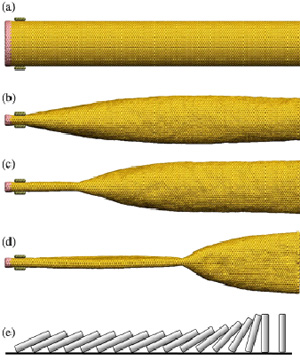
Автору удалось показать, что, сжимая конец углеродной одностенной нанотрубки, можно наблюдать схлопывание остальной ее части. Трубка схлопывается не одновременно по всей своей длине, а последовательно, одно углеродное кольцо за другим, начиная с того конца, который сжали (см. видео). Происходит это подобно тому, как заваливаются кости домино, выстроенные в ряд (это явление известно как «эффект домино»). Только вот роль костей домино здесь выполняют кольца из атомов углерода, образующие нанотрубку, и природа этого явления совершенно иная.

Недавние исследования показали, что у нанотрубок с диаметром от 2 до 6 нм существует два устойчивых состояния равновесия — цилиндрическое (трубка не схлопывается) и сжатое (трубка схлопнулась) — с отличающимися значениями потенциальной энергией, разность которых и может быть использована как источник энергии. Автор установил, что переключение между двумя этими состояниями с последующим высвобождением энергии происходит в виде возникающей доминошной волны. Расчеты ученого показали, что осуществляется такое переключение в углеродных нанотрубках с диметром не 2 нм и более, как следовало из предыдущих исследований, а чуть больше, начиная с 3,5 нм.

Теоретическое исследование «эффекта домино» проводилось с помощью специального метода классической молекулярной динамики, в котором взаимодействие между атомами углерода описывалось с помощью сил Ван-дер-Ваальса (межмолекулярных сил), математически выражаемых потенциалом Леннарда-Джонса (Lennard-Jones potential).

Потенциал взаимодействия между двумя молекулами может быть выражен в виде функции, зависящей от межатомного расстояния r следующим образом:

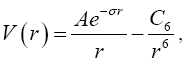
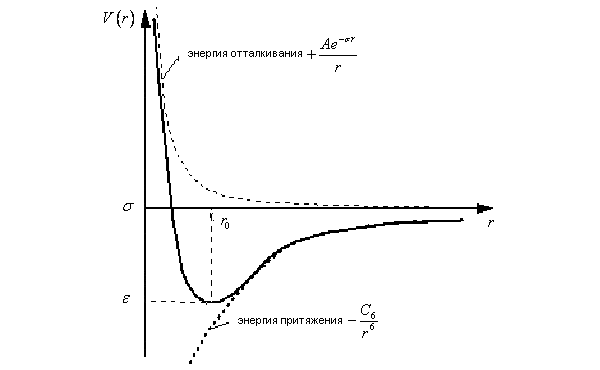
где А и С₆ — некоторые коэффициенты, зависящие от структуры атома или молекулы, ? — наименьшее возможное расстояние между молекулами, e = 2,718... (число e). График такого потенциала представлен ниже на рис. 2. Верхняя (положительная) полуплоскость относительно оси r соответствует отталкиванию молекул, нижняя (отрицательная) полуплоскость — их притяжению. Можно сказать проще: на близких расстояниях молекулы в основном отталкиваются, на дальних — притягиваются. Кстати, на основе этой гипотезы, а теперь уже очевидного факта, Ван-дер-Ваальс и получил свое уравнение состояния реального газа — уравнение Ван-дер-Ваальса.

Рис. 2. График потенциальной энергии межмолекулярного взаимодействия. Изображение с сайта csb.yale.edu

Экспоненциальное слагаемое в выражении для потенциала, описывающее отталкивание молекул на маленьких расстояниях, часто аппроксимируется как 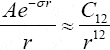. Следовательно, потенциальную энергию взаимодействия молекул можно представить в общем виде как:

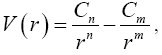
где n и m — целые числа (получаемые экспериментально), C_n и C_m — величины, определяющиеся через равновесное расстояние r₀ между молекулами и глубину «потенциальной ямы» ?; ? и r₀ не являются константами, а имеют значения, характерные для конкретных взаимодействующих частиц (атомов или молекул); так, для атомов углерода глубина «потенциальной ямы» ? в данной статье равна 4,7483 ? 10^–22 Дж (приблизительно 0,003 эВ), а равновесное расстояние r₀ составляет 0,3407 нм. Глубина «потенциальной ямы» ? показывает, насколько «проседает» вниз по оси V(r) энергия межмолекулярного взаимодействия.

Если n = 12, а m = 6, то получаем потенциал Леннарда-Джонса:

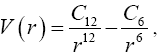
использующийся для математического описания межмолекулярных сил Ван-дер-Ваальса. Потенциал с n = 12, m = 10 может быть использован для описания водородной связи (например, взаимодействия между атомами в молекуле воды).

Поведение углеродной нанотрубки изучалось при комнатной температуре. На рис. 1 показан объект моделирования —углеродная нанотрубка длиной 32 нм с хиральностью (34, 34). Хиральность — это набор из двух целочисленных положительных индексов, который определяет, каким образом сворачивается графитовая плоскость (см. иллюстрацию в Википедии) и сколько элементарных ячеек графита при этом сворачивается, чтобы получить нанотрубку.

Итак, сдавливая с помощью двух плоскостей графена (показаны коричневым цветом на рисунках) один из концов нанотрубки, наблюдаем «эффект домино». Главной причиной обнаруженного эффекта является конкуренция потенциальной энергии ван-дер-ваальсового взаимодействия, которая «коллапсирует» нанотрубку, с энергией упругой деформации, стремящейся сохранить геометрию системы углеродных атомов, что в итоге приводит к бистабильной (схлопнутая и несхлопнутая) конфигурации углеродной нанотрубки.

Для трубки малого диаметра доминирующей является энергия упругой деформации, цилиндрическая форма такой нанотрубки устойчива. Для нанотрубок с достаточно большим диаметром преобладает энергия взаимодействия Ван-дер-Ваальса, что означает большую устойчивость сжатой нанотрубки и меньшую устойчивость, или, как говорят физики, метастабильность (то есть кажущуюся стабильность), ее цилиндрической формы. Таким образом, доминошная волна может родиться в углеродной нанотрубке со сравнительно большим диаметром (более 3,5 нм, как показывают авторские расчеты), так как только в такой системе потенциальная энергия ее схлопывающейся структуры может быть меньше потенциальной энергии «нормальной» нанотрубки. Иными словами, цилиндрическая и схлопывающаяся структура нанотрубки с большим диаметром являются соответственно ее метастабильным и стабильным состояниями.

Рис. 3. (а) Временные зависимости потенциальной энергии и длины схлопнувшейся нанотрубки. (b) Скорость распространения доминошной волны для углеродных нанотрубок с разными диметрами и хиральностью. Максимум скорости (1,28 км/с) наблюдается в нанотрубке диметром около 4,5 нм. Теоретическая зависимость, полученная автором, показана синей сплошной линией. Рисунок из обсуждаемой статьи в Physical Review Letters

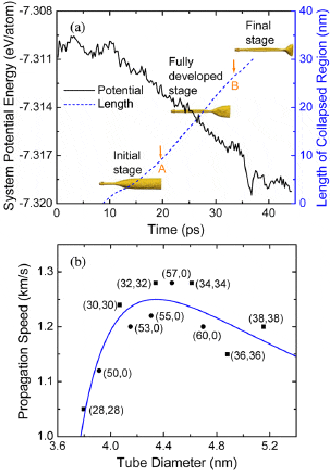
Изменение со временем потенциальной энергии углеродной нанотрубки с распространяющейся по ней доминошной волной представлено в виде графика на рис. 3a.

Этот график указывает на три участка особенностей в изменении потенциальной энергии системы. Первый (от 0 пикосекунд до 10 пс) из них состоит из энергии упругой деформации, появляющейся по причине изменения кривизны стенок нанотрубки в процессе схлопывания, изменения энергии ван-дер-ваальсового взаимодействия, возникающего между противоположными стенками нанотрубки, а также взаимодействия между стенками трубки и графеновыми плоскостями, сжимающими ее конец.

Вторая область (от 10 пс до 35 пс) соответствует уже «эффекту домино» — по поверхности углеродной нанотрубки идет доминошная волна. Энергетически это выглядит так: в каждый момент, когда углеродное кольцо коллапсирует, часть потенциальной энергии взаимодействия Ван-дер-Ваальса переходит в кинетическую энергии (оставшаяся часть — в энергию упругой деформации), которая является своеобразной поддержкой и стимулятором в «падении костей домино» — схлопывании следующих колец, образующих нанотрубку; при этом каждое свернувшееся кольцо уменьшает общую потенциальную энергию системы.

И наконец, третий участок (от 35 пс и до 45 пс) отвечает уже закончившемуся процессу «домино» — углеродная трубка схлопнулась окончательно. Подчеркнем, что нанотрубка, которая схлопнулась (как видно из графика на рис. 3a), обладает меньшей потенциальной энергией, чем было до начала «эффекта домино». Иными словами, распространение доминошной волны — это процесс, идущий с выделением энергии: около 0,01 эВ на один атом углерода. Это, конечно, несопоставимо ни в коей степени с энергетическим выходом в ядерной реакции, но факт генерирования энергии углеродной нанотрубкой очевиден.

Далее в статье автор анализирует кинематические характеристики данного процесса —то есть то, какова скорость распространения волны разрушения или коллапса углеродной нанотрубки и какими характеристиками она определяется? Расчеты показывают, что волна домино в трубке диаметром 4-5 нанометров составляет порядка 1 км/с (как это видно из графика на рис. 3b) и нелинейным образом зависит от ее геометрии — диаметра и хиральности. Максимум эффекта должен наблюдаться в трубке диаметром чуть меньше 4,5 нм — в ней углеродные кольца будут схлопываться со скоростью 1,28 км/с.

Рис. 4. Схема нанопушки, действующей на основе «эффекта домино», в разрезе. (a) Внутри углеродной нанотрубки (55, 0) находится молекула фуллерена С60. Принцип действия можно увидеть в этом видео (см. также пояснения в тексте). (b) Начальное положение и скорость вылета «заряда» (молекулы фуллерена) в зависимости от времени. Наибольшая скорость вылета С60 (1,13 км/с) сравнима со скоростью доминошной волны. Рис. из обсуждаемой статьи в Physical Review Letters

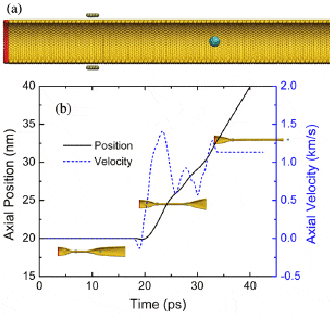
Ну а теперь пример того, как же высвобождающаяся энергия в такой системе с «эффектои домино» может быть применена в наноустройствах. Автор предлагает оригинальный способ использования — «нанопушку» (рис. 4а).

Представим, что в нашем распоряжении находится углеродная нанотрубка с хиральностью (55, 0) и соответствующим для наблюдения эффекта домино диаметром. Поместим внутрь нанотрубки фуллерен С₆₀. Немного фантазии, и можно рассматривать углеродную нанотрубку в качестве ствола пушки, а молекулу С₆₀ — в качестве ее заряда. Расположенная внутри молекула будет под действием схлопывания нанотрубки выдавливаться из нее в другой, открытый, конец (см. видео). Спрашивается, какова скорость такого «ядра»? Чанг рассчитал, что в зависимости от начального положения молекулы фуллерена на вылете из нанотрубки она может достигнуть скорости, близкой к скорости распространения доминошной волны, — около 1 км/с (рис. 4b). Интересно, что эта скорость достигается «ядром» в течение всего лишь 2 пикосекунд и на расстоянии 1 нм. Нетрудно посчитать, что наблюдаемое ускорение имеет огромное значение — 0,5 ? 10¹⁵ м/с². Для сравнения: скорость пули в автомате АК-47 в 1,5 раза ниже скорости фуллерена, вылетающего из такой пушки.

Справедливости ради надо отметить, что моделирование нанопушки проходило в предположении нулевой температуры по шкале Кельвина. Однако, по мнению автора, этот пример не такой уж и абстрактный и вполне может найти применение в инжектирующих устройствах.

Таким образом, впервые была продемонстрирована, пусть пока только теоретически, возможность использования одностенных углеродных нанотрубок в качестве источников энергии.

Источник. Tienchong Chang. Dominoes in Carbon Nanotubes // Physical Review Letters, 101, 175501 (24 October 2008).

Юрий Ерин

<< Назад