Новый параметр поможет предсказывать развитие турбулентности в среде с дисперсными частицами
|
Физикам из Стэнфордского университета США, основываясь на теоретических расчетах и экспериментальных данных, удалось получить новый безразмерный параметр — импульсное число частицы, — который поможет лучше предсказывать развитие турбулентности в среде с дисперсными частицами.
Беспорядочное, бурное движение жидкости, газа или плазмы называется турбулентным, в противоположность спокойному, послойному течению, именуемого ламинарным. Необычность этого явления (турбулентности) заключается в том, что картина течения, например жидкости, постоянно изменяется, даже если внешние условия стабильны во времени.
Законченной теории турбулентности нет и по сей день, хотя попытки ее создать начались еще в конце XIX века, с работ Осборна Рейнольдса. Ему удалось выяснить, что переход от стационарного течения жидкости к меняющемуся во времени происходит, когда некая безразмерная комбинация скорости жидкости, ее вязкости и характерного размера системы, в которой протекает данная жидкость, достигает конкретного значения — критического значения числа Рейнольдса. Обычно по порядку величины оно составляет тысячу, но в специальных условиях можно сохранить ламинарное течение и для намного большего значения критического числа Рейнольдса — 106.
С математической точки зрения турбулентное течение можно описать уравнениями Навье–Стокса, представляющими собой нерешенную до сих пор систему дифференциальных уравнений в частных производных. Эти уравнения с заданными граничными условиями определяют зависимость скорости течения от времени и координат. Интересно, что Институт математики Клэя (см. также статью в Википедии) рассматривает эту задачу как одну из «проблем тысячелетия» — Millennium Problems (на русском языке о «проблемах тысячелетия» можно почитать здесь), назначив за ее решение премию в 1 миллион долларов.
А теперь предположим, что в бурлящую турбулентную среду мы бросаем частички какого-нибудь вещества — скажем, кусочки бумаги в воду или кусочки полиэтилена в воздух. Очевидно, что они будут вовлечены в это вихревое, хаотическое движение. Возникает вопрос: турбулентное течение среды станет более бурным или начнет затухать? Количественно эту задачу можно переформулировать так: увеличивается или уменьшается кинетическая энергия турбулентной среды, когда в нее «вводят» частицы? Вопрос этот имеет не только чисто теоретический интерес. В любой жидкости или газе всегда присутствуют дисперсные частицы. Например, планктон в океане, аэрозоли, каталитические вещества и т. п. Оказывается, что характеристики вроде числа Рейнольдса или числа Стокса в этом случае недостаточно хорошо позволяют оценить влияние частиц на турбулентность в среде, в которой они находятся.
Появлялись работы, в которых в качестве критерия влияния выступало отношение диаметра дисперсной частицы к характерному размеру наибольшего вихря в турбулентной среде. Однако этот подход плох тем, что он не учитывал плотность дисперсных частиц, а также не мог предсказать изменение кинетической энергии турбулентной среды.
Физикам из Стэнфордского университета удалось найти такой оптимальный критерий. В своей статье Classification of Turbulence Modification by Dispersed Spheres Using a Novel Dimensionless Number (статья доступна для скачивания), появившейся недавно в журнале Physics Review Letters, они преобразовали уравнения Навье–Стокса с учетом присутствия в среде дисперсных частиц. В результате всех этих преобразований удалось получить безразмерный параметр наподобие числа Рейнольдса, который с наибольшей точностью позволяет предсказывать влияние дисперсных частиц на развитие турбулентности в среде. Авторы назвали этот параметр «импульсным числом частицы» и обозначили Pa.
Импульсное число частицы можно определить двумя способами:
1) через числа Рейнольдса турбулентной среды и дисперсных частиц (все обозначения авторские):
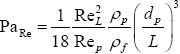
(ReL — число Рейнольдса для данной среды (жидкости, газа и т. п.), Rep — число Рейнольдса дисперсной частицы, ?p — плотность частицы, ?f — плотность потока, dp — характерный размер частицы, скажем, ее диаметр, L — характерный размер турбулентной среды),
2) либо через число Стокса:
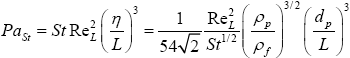 .
.
Добавим, что ? здесь обозначает не вязкость среды (как принято), а так называемый колмогоровский масштаб, то есть размер участка среды, где нельзя пренебречь ее вязкостью. Этот масштаб, установленный в середине прошлого века А. Н. Колмогоровым и А. М. Обуховым, можно приблизительно определить следующим образом:
![]()
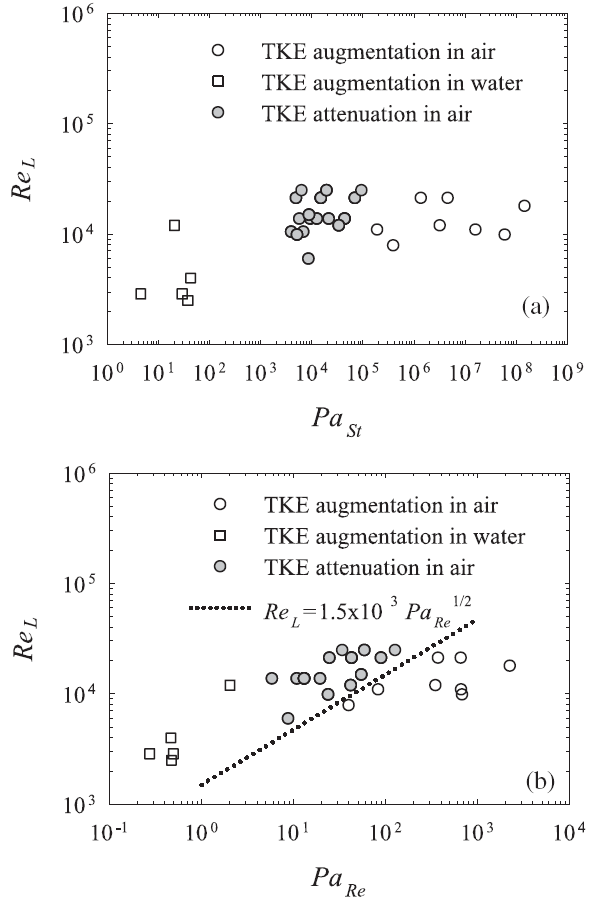
На следующем этапе своего исследования, авторы проанализировали 80 измерений в эксперименте по влиянию частиц на кинетическую энергию турбулентной среды, построив зависимость ReL от специально посчитанного для данного эксперимента импульсного числа Pa, выраженного как через числа Рейнольдса, так и через число Стокса. Использовались лишь те экспериментальные данные, которые показывали более чем пятипроцентное «ослабление» или «усиление» турбулентности (то есть количественное увеличение или уменьшение кинетической энергии).
Графики на рис. 1 позволяют сделать несколько интересных замечаний. Первое — импульсное число частицы действительно хорошо дифференцируют случаи ослабления/усиления турбулентности, при этом число Рейнольдса, как легко видеть, играет совсем незначительную роль, поскольку экспериментальные точки укладываются в своем большинстве на прямую, параллельную оси PaSt (рис. 1a).
Второе — классификация случаев усиления/ослабления турбулентности описывается немонотонной функцией. Частицы с большим значением импульсного числа усиливают турбулентность, частицы с меньшим Ра ослабляют, и, наконец, частицы с еще более маленьким значением Ра снова усиливают хаотическое движение среды. Как видно из графика на примере воздушной среды, если Ра > 105, то происходит усиление, в интервале 103 Pa 5 — ослабление, а при Ра 3 — снова усиление.
Таким образом, основываясь на экспериментальных данных (рис. 1b, точечная линия) и теоретических расчетах, можно сделать вывод, что в среде происходит усиление турбулентности, если выполняется соотношение ReL или PaRe ReL > ![]() и PaRe > 3.
и PaRe > 3.
Конечно, данная работа не решает глобальную проблему описания турбулентности, но свою локальную задачу — максимально точно учесть влияние дисперсных частиц на развитие турбулентности в среде — авторы обсуждаемой работы выполнили.
Источник: Tomohiko Tanaka, John K. Eaton. Classification of Turbulence Modification by Dispersed Spheres Using a Novel Dimensionless Number (полный текст — PDF, 290 Кб) // Physical Review Letters 101, 114502 (2008).