Поляризация воды может происходить под действием теплоты

Рис. 1. «Профиль» теплового потока в исследуемой системе, к которой приложена разность температур 475 и 325 К. Значение теплового потока 2,6·1010 Вт/м2. Слова «горячий» и «холодный» показывают расположение термостатов — в данном случае областей системы с постоянной температурой. Рисунок из обсуждаемой статьи в Phys. Rev. Lett.

Теоретические расчёты физиков показывают, что такой диэлектрик, как вода, можно поляризовать, создав в нём постоянную разность (градиент) температур. При этом электрическое поле в воде может достигать огромного значения — порядка 10⁸ В/м.

Разность температур, приложенная к границам некоторой системы, способна генерировать в ней электрический ток. Это явление физики называют эффект Зеебека. Правда стоит оговориться, что речь идёт о «неоднородной» системе, точнее контакте двух различных металлов. Ясно, что в случае «однородной» системы, когда разность температур приложена к металлу, электрический ток возникать не будет.

Что будет в случае, когда градиент температуры будет создаваться в диэлектрике? Казалось бы, свободных носителей заряда нет, а потому отсутствие электрического тока очевидно. Однако, как оказалось, будет наблюдаться другой электрический эффект — поляризация диэлектрика. Известно, что молекулу диэлектрика можно представить как маленький диполь. В работе Water Polarization under Thermal Gradients норвежских и английских учёных показывается, что дипольные моменты молекул диэлектрика, в котором создаётся постоянная разность температур, упорядочиваются и ориентируются в направлении области с меньшей температурой.

Но обо всём по порядку. Рассматриваемая работа является чисто теоретической и, как понятно из названия, объектом исследований стал наиболее известный диэлектрик — вода. В своих расчётах авторы используют аппарат неравновесной термодинамики, при этом вода заменяется моделью под названием Central Force Model (модель центральной силы). Создаваемый градиент температуры выводит систему из состояния термодинамического равновесия, поэтому использование неравновесной термодинамики оправдано. Чем же тогда обусловлено использование Central Force Model для рассмотрения свойств воды? Всё это необходимо для более упрощённого количественного описания свойств воды, в том числе и в условиях прохождения через неё теплоты. Сама модель центральной силы была предложена сравнительно недавно (в 1975 году) американскими учёными Ховардом Лембергом и Фрэнком Стилинджером. Их работа была опубликована в Journal of Chemical Physics под названием Central-force model for liquid water. Несмотря на упрощения в описании свойств воды в рамках данной модели, доказательством её пригодности может служить тот факт, что посчитанная диэлектрическая проницаемость воды в рамках Central Force Model ?_theor = 82 слабо отличается от экспериментального значения ?_exp = 78,3.

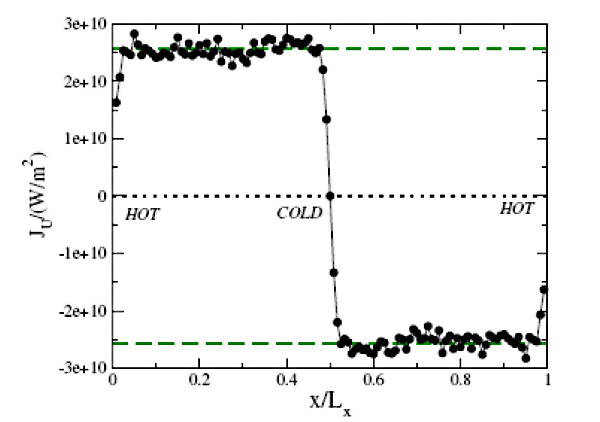
Возвращаясь к обсуждаемой работе, отметим, что исследуемая система представляла собой прямоугольный параллелепипед — «ящик» с размерами L_x = 5L_y = 5L_z, где L_z = 19,73 A или (второй вариант «ящика») L_x = 10L_y = 10L_z, где L_z = 14,79 A, где L_x,y,z — длина, ширина и высота соответственно. В этих ящиках находилось соответственно 1280 и 3240 молекул воды. Градиент температуры создавался вдоль оси х. «Профиль» распространения тепла в системе показан на рисунке 1. Постоянство температур можно регулировать с помощью термостатов, располагая их по бокам и в середине системы.

Предполагается, что температура на торцах моделируемой системы размером L_x = 5L_y = 5L_z составляет 475 К, в середине «ящика» 325 К, что соответствует тепловому потоку 2,6·10¹⁰ Вт/м², либо (второй случай) 450 К и 350 К с тепловым потоком, равным 1,4·10¹⁰ Вт/м². В обоих случаях вода находилась под давлением 1400 атмосфер.

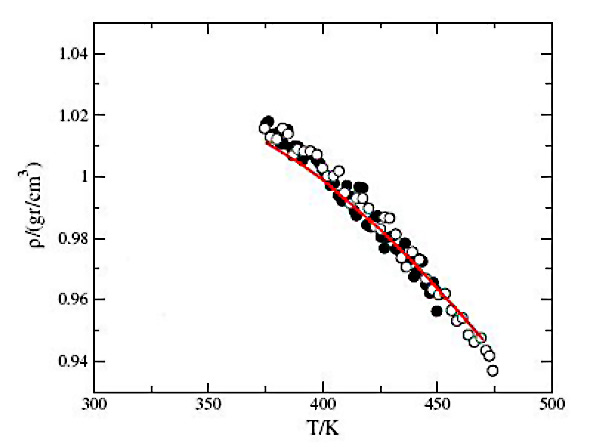
Чтобы проверить, насколько методы неравновесной термодинамики адекватно описывают рассматриваемую систему, находящуюся в таких условиях, авторы рассчитали температурную зависимость плотности воды (рис. 2.).

Рис. 2. Температурная зависимость плотности воды, теоретически рассчитанная в случае, когда тепловой поток равен 2,6·1010 Вт/м2 (пустые круги) и 1,4·1010 Вт/м2 (чёрные круги). Сплошная красная кривая — экспериментальная зависимость. Давление в системе равно 1400 атмосфер. Совпадение теоретических и экспериментальной кривых, по мнению авторов, говорит о применимости методов неравновесной термодинамики для данной задачи. Рисунок из обсуждаемой статьи в Phys. Rev. Lett.

Пустые и зарисованные круги на графике отвечают тепловым потокам 2,6·10¹⁰ Вт/м² и 1,4·10¹⁰ Вт/м² соответственно. Сплошная красная линия — экспериментальная кривая. Как видно, согласие теоретического описания и экспериментальных данных явно просматривается, а значит, в дальнейшем, теоретическая модель, базирующаяся на методах неравновесной термодинамики, должна давать правильные результаты.

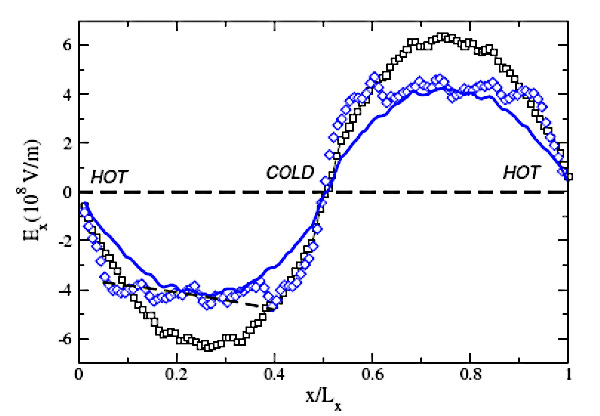
Основной результат работы можно представить в виде графика зависимости напряжённости электрического поля вдоль направления созданного градиента температуры в исследуемой системе (рис. 3).

Рис. 3. Распределение напряжённости электрического поля вдоль направления градиента температуры для случая, когда поток тепла составляет 2,6·1010 Вт/м2 (градиент температуры ?T1=3 К/A ) (чёрные квадраты) и 1,8·1010 Вт/м2 (градиент температуры ?T2=2 К/A) (синие круги). Сплошная синяя линия отвечает напряжённости, создаваемой тепловым потоком 1,8·1010 Вт/м2, полученной с помощью равенства Ex,2 = Ex,1 (?T2/?T1) (см. пояснения в тексте). Рисунок из обсуждаемой статьи в Phys. Rev. Lett.

Здесь чёрными квадратами показана напряжённость электрического поля в системе, когда поток тепла равен 2,6·10¹⁰ Вт/м² (градиент температуры 3 К/A), синими квадратами напряжённость для потока 1,8·10¹⁰ Вт/м² ( градиент температуры 2 К/A). Таким образом, создавая градиент температуры около 10¹⁰ К/м можно создать напряжённость электрического поля в воде порядка величины 10⁸ В/м.

Более того, неравновесная термодинамика предсказывает линейную зависимость между приложенным к системе градиентом температуры ?T и создаваемой напряжённостью электрического поля E_x: 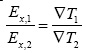. Чтобы проверить это равенство, авторы с его помощью рассчитали зависимость напряжённости электрического поля для теплового потока 1,8·10¹⁰ Вт/м² в предположении, что зависимость E_x (x) для теплового потока 2,6·10¹⁰ Вт/м² известна. Синяя сплошная кривая на рисунке 3 показывает результаты расчета. Нетрудно видеть, что посчитанная ранее координатная зависимость напряжённости электрического поля (синие круги) и зависимость E_x (x) для теплового потока 1,8·10¹⁰ Вт/м², полученная с помощью соотношения, практически совпадают.

В заключении остаётся лишь один вопрос, который необходимо выяснить, а именно, что заставляет молекулы воды упорядочиваться под действием теплоты? Не вдаваясь в подробности сложных понятий неравновесной термодинамики, данный эффект можно объяснить следующим образом: общеизвестно, что любая термодинамическая система, находящаяся в неравновесии с окружающей её средой, стремится найти «устойчивое» состояние. Так вот, благодаря поляризации диэлектрика, система как бы оказывает сопротивление при распространении теплоты, стремясь таким образом скомпенсировать неравномерное распределение температуры внутри себя.

Что касается экспериментальной проверки полученных результатов, то авторами предлагается вариант искать описанную поляризацию не только в воде, но и, например, в наночастицах металла, подвергаемых электромагнитному излучению. В таком случае может быть создан градиент температуры 10⁸ К/м, приводящий к значению напряжённости электрического поля порядка 10⁶ В/м. Подобный эффект может быть также измерен и в биологических клетках. Речь идёт о недавно обнаруженном явлении наблюдения температурного градиента между Са²⁺-АТФазой и окружающим раствором порядка 10⁶ К/м, что должно приводить к возникновению напряжённости электрического поля ~10⁴ В/м.

Источник: Fernando Bresme, Anders Lervik, Dick Bedeaux and Signe Kjelstrup. Water Polarization under Thermal Gradients // Physical Review Letters, 101, 020602 (2008).

Юрий Ерин

<< Назад