Мыльные пузыри помогут предсказывать траектории ураганов

Рис. 1. Примеры проявления двумерной турбулентности в планетарном масштабе. Вверху: снимок урагана Катрина — одного из наиболее разрушительных ураганов в истории США, — сделанный со спутника 29 августа 2005 года. Внизу: снимок Большого красного пятна — атмосферного образования на Юпитере, наблюдаемого уже почти 350 лет, — сделанный Вояджером-1 в 1979 году; см. также видеоролик атмосферных вихрей в районе Большого красного пятна, составленный из 66 снимков (по одному в юпитерианский день). Изображения с сайтов web.mit.edu и ru.wikipedia.org

Исследователи из Центра радиоволн и молекулярной оптики (Centre de Physique Moleculaire Optique et Hertzienne, CPMOH) в Бордо (Франция) обнаружили, что вихри, определенным образом созданные в мыльных пузырях, ведут себя аналогично более масштабным атмосферным явлениям, таким как циклоны и ураганы. Мыльные пузыри дали возможность промоделировать факторы, управляющие траекторией поведения ураганов. Все эти исследования, опубликованные в недавнем выпуске журнала Physical Review Letters, могут помочь лучшему пониманию этих опустошительных атмосферных явлений, участившихся в последнее время.

С физической точки зрения ураганы (циклоны) представляют собой, в планетарном масштабе, пример интереснейшего явления, называемого турбулентностью, — хаотического движения потока жидкости, газа или плазмы с переменными во времени плотностью, скоростью, давлением и температурой. Понятие турбулентного и противоположного ему «послойного», ламинарного течения ввел более ста лет назад английский физик Осборн Рейнольдс, когда изучал движение жидкости в трубе. Позднее его имя было увековечено в виде безразмерной характеристики — числа Рейнольдса — критерия, обозначающего переход от ламинарного движения к беспорядочному, турбулентному.

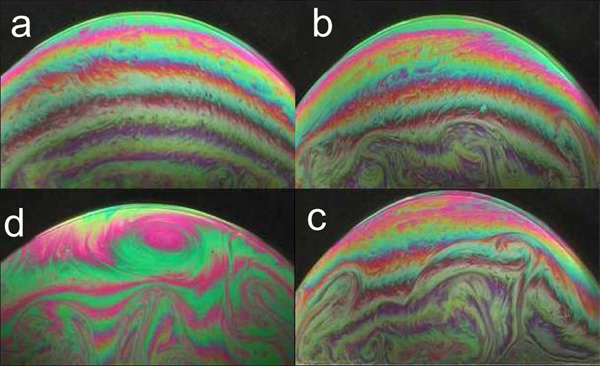
Поскольку турбулентность представляет собой явление со случайным образом изменяющимися параметрами, то построение математической модели должно основываться на усреднении этих характеристик во временном интервале. Если геометрия системы, в которой изучается турбулентность, имеет некую симметрию, то возможно перейти от изучения трехмерной модели этого явления к двумерной; это позволяет упростить математику задачи. Ураганы — именно тот случай, когда можно этим упрощением воспользоваться (рис. 1).

Разумеется, в лабораторных условиях моделировать зарождение ураганов сложно по причине их немаленьких размеров (о том, как зарождаются ураганы, можно почитать в статье Ураганы — вечная проблема, «Наука и жизнь» №3, 2006). Поэтому французские ученые в своей работе Thermal Convection and Emergence of Isolated Vortices in Soap Bubbles предложили оригинальный эксперимент с мыльными пузырями, практически равноценно заменяющий эти атмосферные явления. Вообще говоря, мыльные пузыри — идеальная модель для изучения турбулентности в газовых оболочках планет, так как по своим физическим параметрам отношение толщины мыльной пленки к диаметру пузыря эквивалентно отношению толщины атмосферы к диаметру планеты.

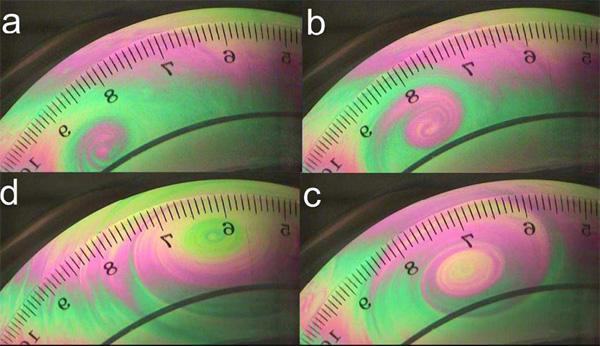
Постановка эксперимента французских ученых очень простая. Половина мыльного пузыря, находящегося при комнатной температуре 17°C, с радиусом в разных вариациях эксперимента от 8 до 10 см, нагревалась с помощью специального колечка, охватывающего экватор пузыря. Тепло конвективным образом распространялось от экватора к полюсам, создавая градиент (разность) температур ?T. Облучая изучаемый объект белом светом, исследователи наблюдали интерференционную картину, из которой видно, что при наибольшей разности температур между экватором и полюсом происходило зарождение вихря, подобного атмосферному циклону (см. рис. 1, 2). Интерференционная картина в эксперименте — это своеобразная визуализация конвективного распространения тепла по поверхности пузыря. Она возникает вследствие того, что белый свет из-за неоднородности в толщине пленки, обусловленной в свою очередь неодинаковым нагревом, «по-разному» преломляется и отражается в мыльном пузыре.

Рис. 2. Изображения пузырей при различных температурных градиентах. Разность температур ?T увеличивается от рис. a к c и равно 9, 17 и 31°C соответственно. На рис. d: возникновение вихря при ?T = 45°C. Рис. из обсуждаемой статьи в Phys. Rev. Lett.

Подобные эксперименты по моделированию двумерной турбулентности проводились и ранее, но только объектом исследования служила плоская мыльная пленка. Поэтому в заслугу себе авторы ставят то, что они первыми исследовали двумерную турбулентность в такой геометрии (в мыльных пузырях) и, как они отмечают, несмотря на похожие ранее результаты, смогли наблюдать и некоторые особенности турбулентности в такой системе.

Целью французских ученых было измерение различных характеристик пузыря и вихря. Речь идет о толщине пленки в области, где расположился вихрь в данный момент, а также о его размере, скорости, времени зарождения и среднеквадратичном перемещении по поверхности пузыря.

На последней характеристике остановимся более подробно. Разумеется, если следить за координатами вихря, то усмотреть закономерность в его движении очень сложно — процесс-то хаотический. Поэтому для описания динамики такого процесса часто используют понятие среднеквадратичного перемещения точки, частицы, объекта, которые движутся случайным образом.

Самый известный пример — это броуновское движение — тепловое движение микроскопических частиц, находящихся в жидкой или газообразной среде. Теорию этого явления параллельно разработали Мариан Смолуховский и Альберт Эйнштейн, для которого это была первая научная работа. Если мы будем следить за частицей и в определенные моменты времени фиксировать ее координаты r₁, r₂, ..., r_n (n должно быть большим числом), а потом возьмем их среднее арифметическое, то получится ноль: ‹r› = 0. А вот теперь, если мы посчитаем среднеквадратичное значение координат , то, согласно теории Смолуховского–Эйнштейна, через достаточно большой промежуток времени (t) среднеквадратичное значение смещения частицы будет пропорционально времени наблюдения ‹r²› ~ t. Таким образом, некоторая закономерность в броуновском движении существует.

Рис. 3. Рождение и рост вихря. Временные интервалы между снимками составляют 0,16, 0,44 и 0,76 секунды соответственно. На заднем плане показана линейка для сопоставления размера зарождающегося вихря. Видеофрагмент эксперимента можно увидеть здесь

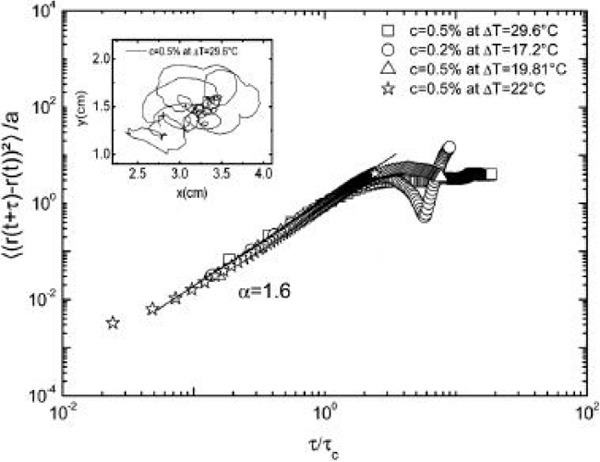
Анализ данных по движению вихрей на поверхности пузыря показал, что такая же закономерность существует и для них. Закон, описывающий их среднеквадратичное смещение, отличается от закона для броуновского движения (что, в принципе, и неудивительно) и выглядит так: ‹r²› ~ t^?, где ? = 1,6. На рис. 4 представлена графическая интерпретация данных, полученных исследователями, — зависимость среднеквадратичного смещения вихрей от времени.

Рис. 4. Зависимость среднеквадратичного смещения ‹r2(?)› вихря от времени ? для различных температурных градиентов ?T и различных концентраций c мыльного раствора (? и ?c — некоторые числа). На вставке: траектория движения вихря. Изображение из обсуждаемой статьи в Phys. Rev. Lett.

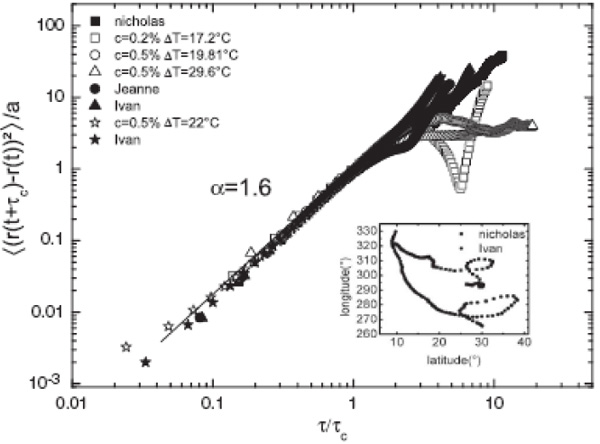
Так при чем же здесь ураганы и какая взаимосвязь между ними и вихрями на мыльных пузырях? Оказывается, что, если посчитать зависимость среднеквадратичного смещения от времени для таких известных ураганов, как, например, Иван, Николас и Джин (данные были взяты авторами с сайта Национального центра США по слежению за ураганами) и сравнить их с аналогичной зависимостью для некоторых вихрей в описанном выше эксперименте (при этом, конечно же, уменьшив масштаб), то будет наблюдаться практически идеальное согласие на начальном временном интервале (см. рис. 5). Таким образом, математически установлена связь между поведением вихрей в мыльных пленках и ураганов в атмосфере.

Рис. 5. Зависимость среднеквадратичного смещения ‹r2(?)› от времени ? для некоторых ураганов, названия которых указаны на графике, и некоторых вихрей, наблюдавшихся в эксперименте. Нижняя вставка: траектории ураганов Николас и Иван. Обозначения те же, что и на рис. 4. Изображение из обсуждаемой статьи в Phys. Rev. Lett.

По мнению авторов работы, модель вихрей на поверхности мыльных пленок должны также помочь более глубокому пониманию явления турбулентности и, в частности, изучению атмосферных циклонов.

Видеорепортаж об этой работе (на французском языке) можно посмотреть здесь (надо выбрать третий сюжет — «Les bulles de savon: une cle pour comprendre les ouragans!»).

Источник: F. Seychelles, Y. Amarouchene, M. Bessafi, H. Kellay. Thermal Convection and Emergence of Isolated Vortices in Soap Bubbles // Phys. Rev. Lett. 100, 144501 (7 April 2008).

<< Назад