Виды могут конкурировать по принципу «камень–ножницы–бумага»
|
Межвидовые отношения, построенные по принципу игры «камень–ножницы–бумага» (каждый вид контролирует рост численности какого-то другого вида, но сам при этом находится под контролем третьего), по-видимому, действительно встречаются в природе. Математическая модель становления сообщества разных видов, связанных подобным образом, показывает, что при размножении видов и расселении их по поверхности субстрата формируется сложная пространственная структура — чередование участков, занятых разными видами. Если подвижность видов возрастает, то эта структура разрушается: сосуществование видов становится невозможным, а в сообществе остается только один из видов.
Камень «бьет» (тупит) ножницы, ножницы «бьют» (режут) бумагу, а бумага «бьет» (обертывает и обезвреживает) камень. Детская игра «камень–ножницы–бумага» неожиданным образом всё чаще фигурирует в работах экологов как модель взаимоотношений разных организмов. По-видимому, такие связи встречаются достаточно часто среди микроскопических организмов, обрастающих сплошным ковром какие-нибудь поверхности под водой и конкурирующих за место на субстрате. Сосуществование их, по сути противоречащее принципу «конкурентного исключения» («закону Гаузе»), оказывается возможным благодаря реализации принципа «камень–ножницы–бумага». Конечно, у организмов должны быть средства воздействия на своих конкурентов (чем «бить»). Такими средствами служат как правило специальные вещества, продуцируемые и выделяемые в окружающую среду одними организмами для торможения роста и даже уничтожения других.
Примером подобных веществ могут быть антибиотики. Недаром Георгий Францевич Гаузе, получивший в нашей стране первый антибиотик, первоначально занимался лабораторными и теоретическими исследованиями конкуренции и стал известен во всём мире как создатель экспериментальной экологии.
В одной из математических моделей (Czaran et al. 2002), построенных по принципу «камень–ножницы–бумага», рассматривается популяция бактерий, в которой появляется штамм «киллера». «Киллер» вырабатывает токсин, с помощью которого он уничтожает конкурентов и высвобождает пространство для роста собственных колоний. Однако, согласно модели, через некоторое время в популяции появляется «резистентный» штамм, устойчивый к действию токсина «киллера». Кроме того, в среде (точнее, в модели) продолжает существовать исходный «чувствительный» штамм. Выживание последнего обеспечивается очень высокой скоростью его размножения — ведь ему не надо расходовать ресурсы ни на производство токсина, ни на средства его нейтрализации. Скорость размножения «киллера», наоборот, наиболее низкая из всех трёх штаммов (из-за трат на токсин и на защиту от него собственного организма). Скорость размножения «резистентного» штамма — промежуточная между «киллером» и «чувствительным»: он несет расходы на выработку противоядия, но не на сам токсин. Математическая модель такого сообщества из трёх штаммов (видов), растущих на поверхности питательного субстрата и фактически конкурирующих за пространство обитания, показывает, что устойчивое сосуществование видов со временем достигается. При этом участки, занятые разными видами, образуют своего рода чересполосицу.
Есть и некоторые экспериментальные данные, свидетельствующие о реальности подобного способа сосуществования конкурентов. В частности, некоторые штаммы бактерий Escherichia coli (модельный вид во многих лабораторных исследованиях) способны образовывать специальное вещество — колицин (см. также Bacteriocin), тормозящее рост конкурентов. Скорость размножения штамма, производящего колицин, существенно ниже, чем обычного. Поэтому реализовать свои преимущества он может, только если конкуренция разворачивается на поверхности питательного субстрата (агар-агара). В условиях же жидкой перемешиваемой среды он терпит фиаско — выделяемый токсин уносится течением, а скорость размножения обычного штамма гораздо выше.
|
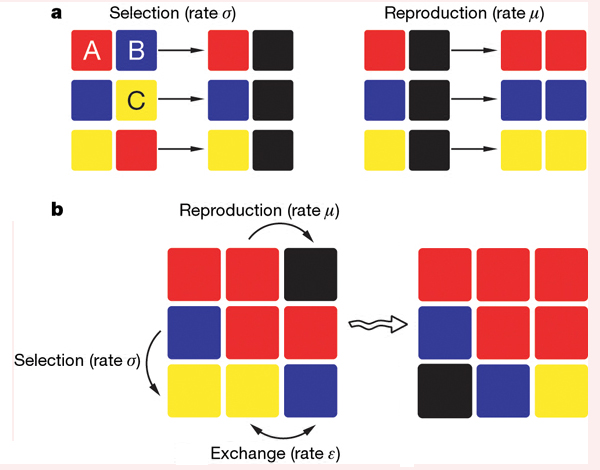
Недавно проблема устойчивого сосуществования конкурентов, связанных отношениями типа «камень–ножницы–бумага», стала предметом специального исследования Тобиаса Райхенбаха (Tobias Reichenbach) — студента из Центра теоретической физики имени Арнольда Зоммерфельда (Университет Людвига Максимилиана, Мюнхен, Германия). Совместно с коллегами из того же центра он предложил модель, в которой три вида размножаются и расселяются по поверхности субстрата — решетки, отдельные ячейки которой могут быть заняты особями только одного вида (см. рис. 1). По условиям модели A «бьёт» (уничтожает в соседней ячейке) B, B – C, а C – A. Процесс уничтожения одного вида другим характеризуется определенной скоростью. Кроме того, в модели задается также скорость размножения видов и их «мобильность» — скорость передвижения из одной ячейки в другую (свободную или же освобождающуюся путем взаимообмена «местом жительства»).
|
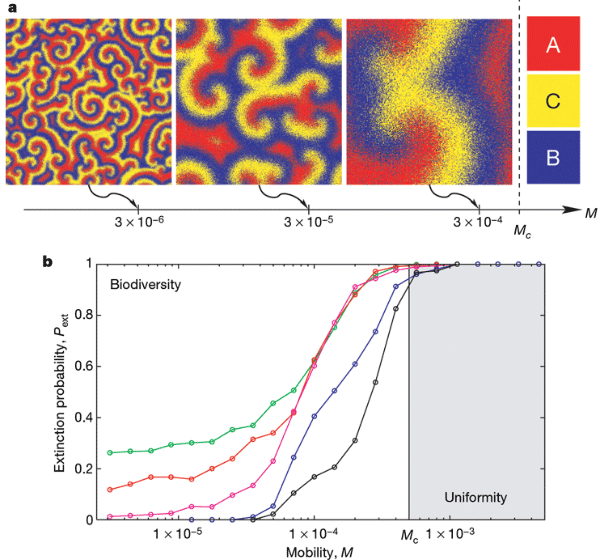
Именно мобильность, согласно выводам работы, оказывается ключевым параметром, определяющим возможность или невозможность сосуществования конкурентов. Хотя некий минимальный уровень мобильности необходим (размножающиеся организмы должны расселяться в свободные ячейки), по мере возрастания мобильности видов вероятность их устойчивого сосуществования снижается. При достижении же некоторой критической величины мобильности в системе остается только один вид (см. рис. 2). Пространственная структура всего сообщества, формирующаяся по мере его развития, выглядит как набор спиралей (или, точнее, «вихрей»), образованных чередованием участков, занятых разными видами. С возрастанием мобильности эти вихреобразные структуры становятся всё более крупными. В конце концов на участке остается пространство, занятое только одним из трёх видов (рис. 2).
Видеоролики в приложении к статье показывают результаты моделирования двух стадий становления сообщества из трех видов — когда мобильность мала и сосуществование стабильно (ролик 1, 9,5 Мб) и когда мобильность близка к критическому значению, но сосуществование еще остается стабильным (ролик 2, 9,5 Мб).
Российскому читателю, наверное, приятно узнать, что при аналитическом решении уравнений, описывающих сложную пространственную структуру сообществ, авторы использовали теорию, разработанную нашими соотечественниками В. Л. Гинзбургом и Л. Д. Ландау (см.: уравнения Гинзбурга–Ландау, а также: The world of the complex Ginzburg–Landau equation, Pdf, 2,4 Мб).
Важно подчеркнуть, что работы, подобные обсуждаемой, не отменяют принципа конкурентного исключения, согласно которому два вида не могут сосуществовать, если они ограничены одним ресурсом. Надо просто иметь в виду, что в моделях Вольтерры и Лотки пространство никак не фигурировало или же взаимодействия видов напоминали столкновения молекул в жидкой среде. Сейчас же становится ясно, что сосуществование конкурирующих видов значительно легче достигается, если их взаимодействие происходит на твердой поверхности (например, в наземных растительных сообществах или среди обрастаний под водой), а не в жидкой перемешиваемой среде (случай планктонного сообщества). В последнем случае конкурентное исключение, по-видимому, действительно происходит гораздо чаще.
Источник: Tobias Reichenbach, Mauro Mobilia, Erwin Frey. Mobility promotes and jeopardizes biodiversity in rock–paper–scissors games // Nature. 2007. V. 448. P. 1046–1049.