Обнаружен эффект памяти в поведении пузырьков воздуха под водой
|
Открыто новое явление в гидродинамике: эффект памяти формы при отрыве от поверхности пузырьков воздуха под водой. Гидродинамические течения, движимые сингулярностями, но обладающие памятью, встречаются физикам впервые.
Капли воды, просачивающиеся через плохо закрытый кран, получаются круглыми вне зависимости от того, было ли выходное отверстие круглое, треугольное или же имело какую-то более сложную форму. Это неудивительно, поскольку поверхностное натяжение и вязкость как раз стремятся превратить любую исходную форму в круглую. Можно сказать, что под действием этих сил вода «забывает» свое начальное состояние.
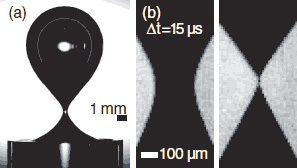
В процессе образования капли есть, однако, один интригующий этап, детали которого до сих пор не до конца изучены. За считанные мгновения до отрыва капли её основная масса уже движется вниз под действием силы тяжести, а с исходной поверхностью её соединяет лишь узкий перешеек. При приближении к моменту отрыва этот перешеек вытягивается и утончается до атомных размеров и наконец рвется.
|
Теоретические вычисления предсказывали, что процесс утончения перешейка тоже характеризуется потерей памяти о первоначальной форме. Не важно, каково было выходное отверстие: перешеек быстро принимал осесимметричную форму. Развитая в последние десятилетия прошлого века технология сверхскоростной видеосъемки (с частотой свыше 100 тысяч кадров в секунду) подтвердила в общих чертах правильность этого вывода.
Сам факт, что течения вязкой жидкости приводят к потере первоначальной формы, казался настолько естественным, что противоречащие ему экспериментальные результаты, полученные в 2003 году исследователями из Университета Чикаго и опубликованные в статье P. Doshi et al., Science, 302, 1185 (2003), были встречены физиками с нескрываемым удивлением. Оказалось, что при отрыве капли воды не в воздухе, а внутри другой, более вязкой жидкости, форма перешейка сильно зависит от формы отверстия, из которого просачивается вода. Напрашивался вывод, что более важную роль в этом процессе играет не сама та жидкость, которая «каплет», сколько среда, внутри которой это происходит.
Последние исследования этой же группы из Чикаго, описанные в статье N. C. Keim et al., Physical Review Letters, 97, 144503 (3 October 2006), доступной также как cond-mat/0605669, можно считать естественным продолжением этого открытия. В них экспериментально изучался отрыв пузырьков воздуха в воде — ситуация, в которой роль окружающей каплю среды сведена к минимуму.
Пузырьки воздуха получались в эксперименте с помощью погруженного в воду и направленного вверх шприца с различными насадками: круглой, овальной и насадкой с профилем в форме полумесяца. Вся установка располагалась на платформе, которую можно было при необходимости наклонять на требуемый угол. Поведение пузырьков фиксировалось на камеру "Phantom" version 7, позволявшей получать до 130 000 снимков в секунду, и затем обрабатывалось компьютером.
|
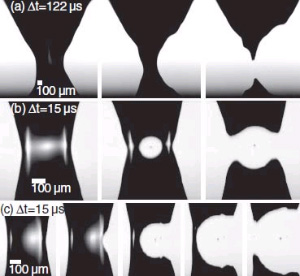
Авторы выяснили, что «классический» сценарий разрыва перешейка (строгая цилиндрическая симметрия и утончение до субмикронных размеров) реализуется только в очень специальных условиях: при строго круглой насадке и абсолютно вертикальной её ориентации. Достаточно взять насадку с чуть вытянутым профилем или же слегка — всего на пару градусов! — наклонить установку, как процесс преображается. Перешеек искажается в направлении вытянутости, принимает плоскую лентообразную форму вместо цилиндрической и затем резко разрывается.
Насадка с еще более несимметричным профилем — в форме полумесяца — производила пузырьки, которые соединялись с ней желобкообразными перешейками. Эта форма сохранялась на протяжении всего процесса утончения и, как показывают снимки, разрыв происходил сразу в нескольких местах.
Иными словами, форма перешейка, соединяющего каплю с поверхностью, повторяет форму выходного отверстия и сохраняется практически неизменной при сужении «перетяжки» в сотни раз! Значит, в этом случае гидродинамические течения не только не «стирают» память о первоначальной форме, но и тщательно её сохраняют. Гидродинамические течения со столь необычными свойствами физикам до сих пор не встречались.
Стоит отметить, что в этой истории физиков-теоретиков больше беспокоит не само по себе необычное поведение воды, а тот факт, что определенный математический прием, часто используемый в теоретической физике, на этот раз дал осечку. Речь идет о выделении доминирующей сингулярности при изучении поведения решений уравнений эволюции. Дифференциальные уравнения, описывающие эволюцию какой-либо системы во времени, могут быть очень сложными, но при приближении к «катастрофическому» моменту (в данном случае — к моменту разрыва перешейка) они, как правило, существенно упрощаются. Обычно удается выделить ту главную силу, которая толкает систему к катастрофе, а всё остальное при этом становится второстепенным. В этом случае поведение системы вблизи критического момента обычно ничего не «помнит» о начальных условиях просто потому, что главная сингулярность слишком проста, чтоб вобрать в себя эту информацию.
В данном случае эксперименты показали, что система ведет себя самоподобно — что характерно для систем, движимых какой-то одной главной сингулярностью, — но при этом информация о начальном состоянии сохраняется в течение всей эволюции. Что это за сингулярность, которая умудряется быть одновременно столь простой и столь информационно емкой, физикам и предстоит разобраться.
Не исключено, что эти, казалось бы, чисто математические тонкости вскоре отразятся и на прикладной физике или даже на современных технологиях. Образование и отрыв капелек и пузырьков используется повсеместно, начиная с химической промышленности и заканчивая струйными принтерами. Теоретическое моделирование таких процессов, которое предваряет их внедрение в технологии, до сих пор игнорировало саму возможность подобных эффектов памяти. Для физика же эта работа является лишним подтверждением того, что несмотря на многовековую историю гидродинамики, нестационарные течения со свободной поверхностью до сих пор таят в себе немало сюрпризов (о другом примере мы писали недавно в заметке Бурная жизнь длиной в сантиметр).
Игорь Иванов